Number Bases, Numbers
and
The Right Side of Mathematics
Han Erim
7 November 2015
Right Side in mathematics is an alternative interpretation of number
bases. In this interpretation, the number 1 belonging to base 1 is the
largest number. The values of the number elements belonging to bases are
formed according to the number/base rule.
Right Side number bases and numbers have been defined with this study
and have gained a foundation.
The Left Side of Mathematics
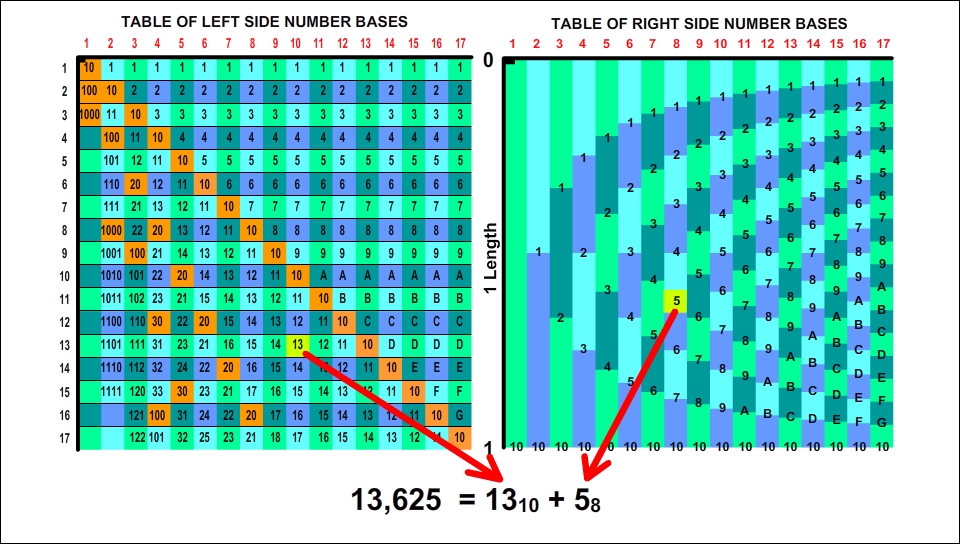
When we define something as the Right Side in mathematics, it is
naturally necessary first to explain what the Left Side means in
mathematics. The Left Side represents the normal arrangement of number
bases as we currently use them. The table below shows the arrangement of
numbers within the Left Side. Normally, we consider and use number bases
and numbers in the classical form shown in this table.
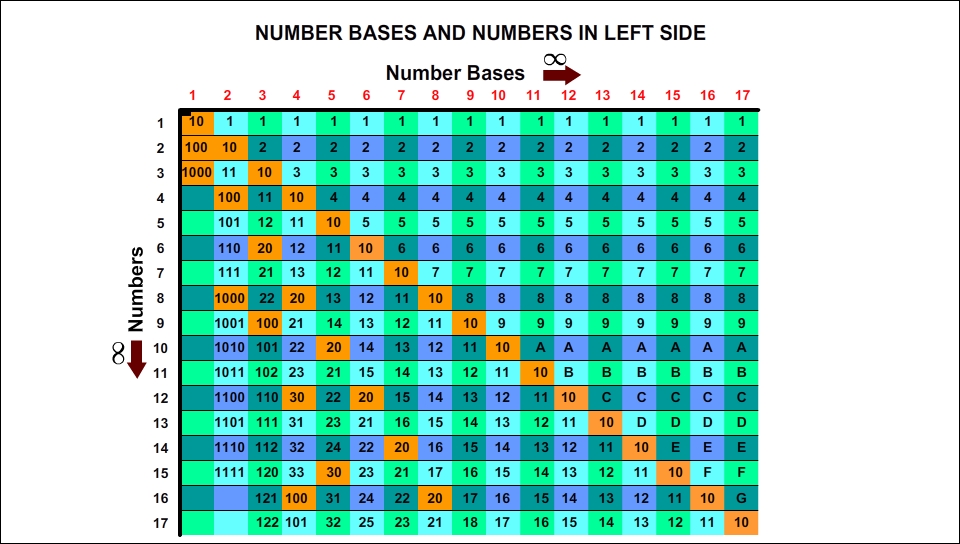
As we know, in daily life we use the base 10 number system. Base 10
consists of 10 elements (0,1,2,3,4,5,6,7,8,9). In addition, some number
bases such as Binary (base 2) and Hexadecimal (base 16) are frequently
used in programming and mathematical calculations.
Any number can be written according to any base. For example, the
representation of the number "127" in some number bases is as follows:
| Binary (Base 2) |
111 1111 |
| Octal (Base 8) |
177 |
| Decimal (Base 10) |
127 |
| Hexadecimal (Base 16) |
7F |
| Base 4 |
1333 |
| Base 23 |
5C |
The expansion rule of a number according to its base is as follows:
In the examples, the expansions of the number 127 in base 10 and base 4
are shown.
BASE 1
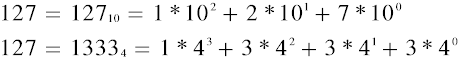
Although it is not used on the Left Side at all, Base 1 is extremely
important for the Right Side. Base 1 consists of a single element, but
in order to express it, a second auxiliary number is also needed. For
this, the number 0 is used. Numbers in Base 1 can be represented in two
ways.
| Number Value |
1st Representation |
2nd Representation |
| 1 |
1 |
10 |
| 2 |
11 |
100 |
| 3 |
111 |
1000 |
| 4 |
1111 |
10000 |
As seen in the table, in the 1st representation we write the digit 1
repeatedly as many times as the number value.
In the 2nd representation, we append zeros consecutively as many times
as the number value, and add a 1 at the beginning.
In this study, both representation methods are used. For example, in
the main table above, for compatibility with the table, the second
representation method was preferred.
The numbers that are elements of a number base always have values
smaller than the base value. For example, base 2 consists of (0,1), base
6 consists of (0,1,2,3,4,5), and base 16, called Hexadecimal, consists
of the elements (0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F).
However, out of necessity and as an exception, in base 1 the digit 1 is
used both as a number value and as a base value. That is, in base 1,
representations such as 11, 101, 1111 are used.
Because it is impractical for mathematical calculations, the base 1
number system is not used on the Left Side. However, calculations can
still be performed using this number base.
As an example, the operation 3 + 2 = 5 in base 1 is as follows:
According to the 1st representation: 1111 + 111 = 111111
According to the 2nd representation: 10001 + 1001 = 1000001
DERIVATION OF RIGHT SIDE NUMBER BASES
The comparative table below shows the difference between Left Side and
Right Side number bases.
(The values in the table have been arranged according to the decimal
system by ignoring the number writing rules.)
As can be seen, Right Side numbers are formed by the rule
11 = 2×12 = 3×13
= 4×14 ... = (n-1)×1n-1 = n×1n.
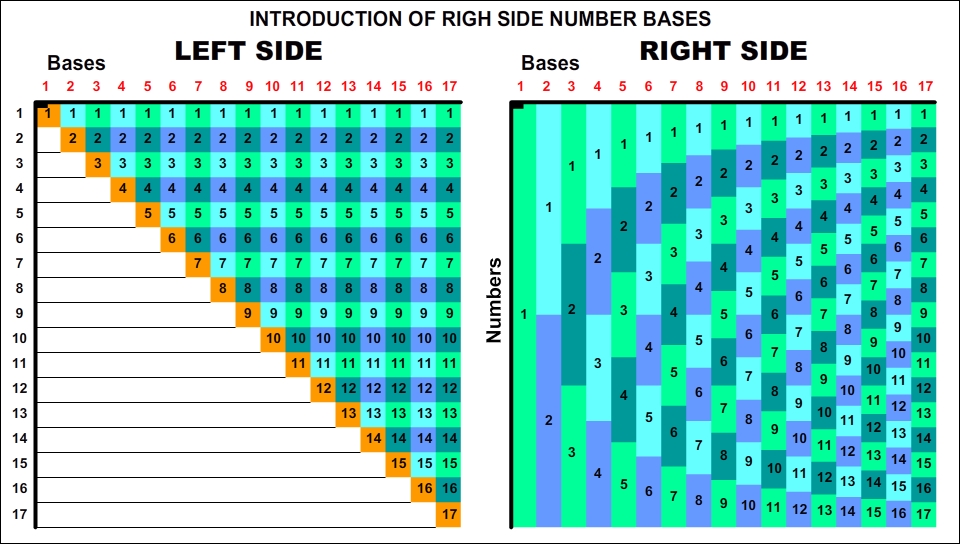
Below is the version of the table above prepared in accordance with the
number writing rules. By adding a geometric interpretation, the numbers
have been positioned vertically in proportion to the values they
represent.
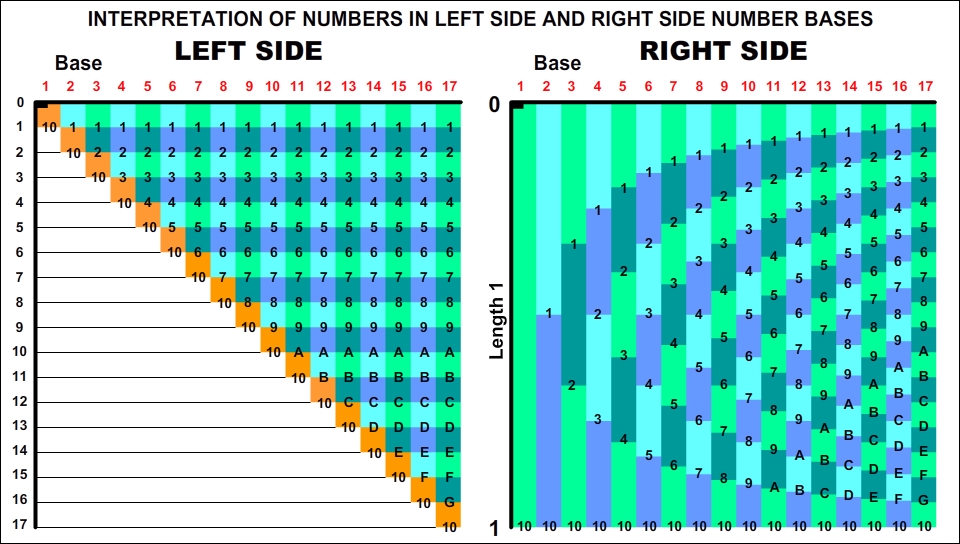
Within the Right Side table, all numbers remain within the length of the
number 1
1.
|
Definition of Length of 1:
In the Right Side number bases table,
the length that represents the number 11
in base 1 and at the same time indicates the 0–1 interval
is called the Length of 1.
|
Position and Numerical Value of Right Side Numbers on the Length of 1:
On the Right Side, a number is positioned at a fixed point on the
Length of 1 and is located in proportion to numberValue/base,
according to the value it contains.
For example, the number 2 in base 6 is at the point 0.333... of the
Length of 1, while the number 3 in base 8 is at the point 0.375. The
position point is also the true numerical value of the number.
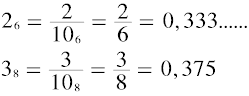
(The Left Side counterparts of the same numbers are: 26 = 2 and 38
= 3.)
In the table below, we can comparatively observe the main characters of
Left Side and Right Side numbers:
| LEFT SIDE NUMBERS |
RIGHT SIDE NUMBERS |
11 = 12 = 13
= ... = 1n
ab = ac = ad = a
101 < 102 < 103 ... < 10n
|
11 > 12
> 13 ... > 1n
ab = a/b, ac = a/c, ad = a/d
101 = 102 = 103 ... = 10n |
| Here, a, b, c, d, n are integers. |
Fractional Representation of Right Side Numbers
On the Right Side, the fractional representation is obtained by writing
the base values as the denominator values of the number elements.
The table below shows two different representations of Right Side Number
Bases: natural and fractional.
In the fractional representation, the decimal number system is used for
the numerator and denominator for convenience. However, it can also be
shown in accordance with the number writing rules.
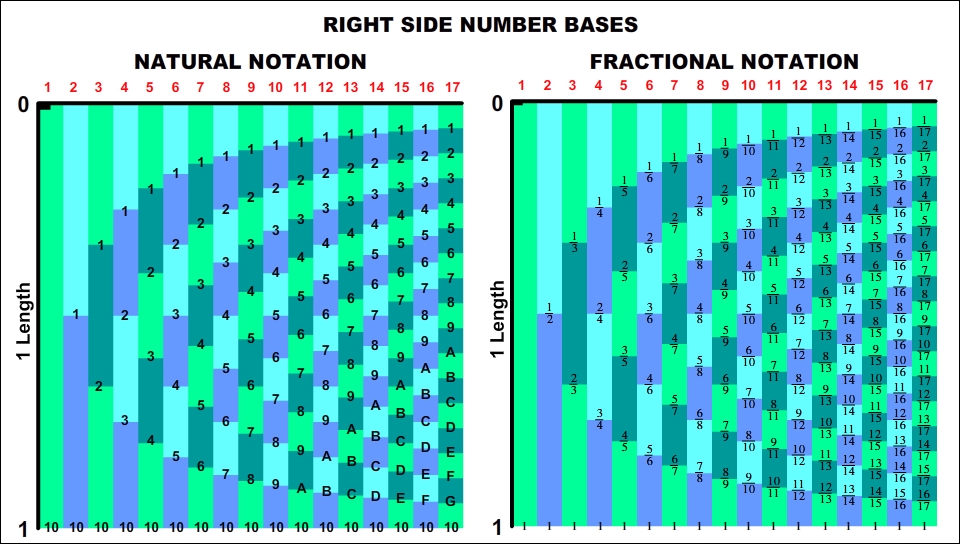
Natural Representation of Right Side numbers: 26, 813,
5866, ...
Fractional Representation of Right Side numbers: 2/6, 8/13, 58/66, ...
Connection Between Left Side and Right Side
In order to build a bridge between the two sides, it is accepted that
the number 11 belonging to base 1 on the Left Side is equal to
the number 11 belonging to base 1 on the Right Side.
Therefore, the Length of 1 on the Right Side is equal to the number 1 on
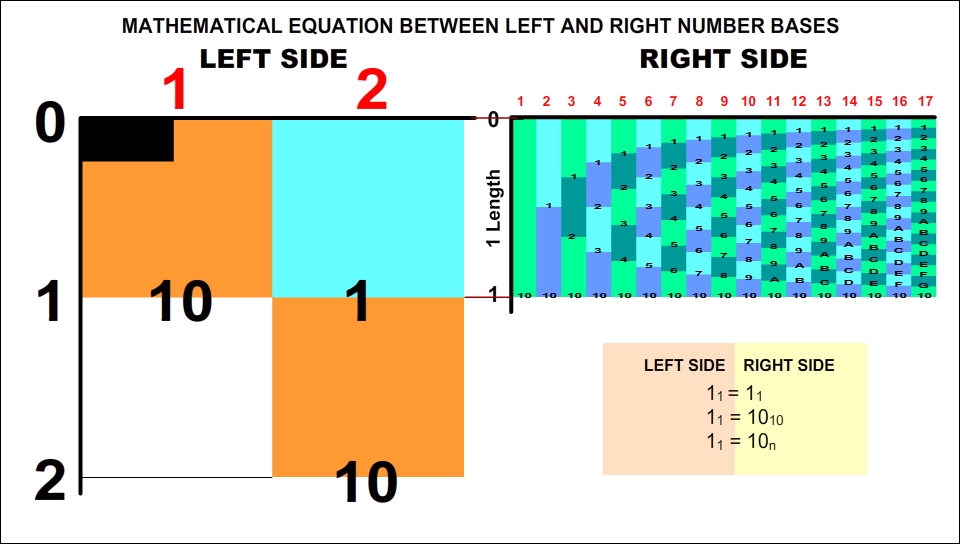
the Left Side.
Left Side and Right Side Components of a Number
The value of a number that is equal to one or greater than one is the
Left Side component of the number; the values smaller than one are the
Right Side component.
For example, in the number 19.375:
The integer 19 on the left of the decimal point is the Left Side component:
1910 (Left Side)
The value 0.375 on the right of the decimal point is the Right Side component.
Since 0.375 = 3/8, it is expressed on the Right Side as 38.
Result:
19.375 = 1910 (Left Side) + 38 (Right Side)
Other examples:
2.333... = 2 + 0.333... = 2 + 1/3 = 210 (Left Side) + 13
(Right Side)
8.5 = 8 + 0.5 = 8 + 1/2 = 810 (Left Side) + 12
(Right Side)
Right Side Representation for Irrational Numbers
In irrational numbers, the numerator and denominator values in the Right
Side fraction extend to infinity.
For this reason, fractions are expressed with approximate values.
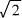≈ 1 +
0.4142 ≈ 1 + 6625109/15994428
That is:
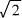≈ 110
(Left Side) + 662510915994428 (Right Side)
Similarly:
π ≈ 3 + 0.1415 ≈ 3 + 29629644/209259755
π ≈ 310 (Left Side) + 29629644209259755 (Right Side)
| As a result, all numbers in the 0–1 interval are Right Side
numbers. The value of a number consists of the sum of the Left Side
component and the Right Side component. |
A few final remarks on Right Side number bases and numbers
The Right Side is a comprehensive subject that needs to be researched.
Due to its interesting structure, I think it is possible to produce
different algorithms and solutions by using Right Side number bases and
numbers.
If mathematicians work on this subject, they will reach very interesting
findings.
The best outcome of Right Side mathematics for me is that it led me to my
work in physics, which I named the Alice Law.
Thank you for reading.
Han Erim