















21. TIME SHIFT

The wavelength change in the electromagnetic interaction between objects that are in motion relative to each other changes the speed of flow of Visible Time. This event is called Time Shift.

In my previous studies, I dealt with and published the event Time Shift under different names (Time Dilation, Time Deformation). However, I believe the best name is Time Shift. Together with this new name, the close relationship between Time Shift and Doppler Shift is emphasized.

Let’s assume that you are looking at your watch on your wrist. If you move your arm while looking at it, the flow rate of time that the watch shows you immediately changes. If you move the watch away from your face, you will see that the watch is working slowly; and if you bring it closer to your face, you will see that it is working fast. This change has nothing to do with the mechanism of the watch. The watch works at the same speed. The change occurs on the Image Object of the watch and, since you are seeing the Image Object of the watch and not the Source Object, you see the watch speed up or slow down. Of course, this change is too little to notice; the distance is too short and the movement of your arm is too slow. However, this change indeed occurs. Now, let’s see how Time Shift occurs by increasing distance and speed.

We cannot see a clock from a few hundred meters with our eyes. But we can follow the following method: Let’s observe a clock from through a camera and broadcast the image of the clock live. Such a setup will be no different than looking at the watch on our wrists. Even if we are in motion, we can observe the clock from hundreds, even thousands of kilometers away. To make it easy to understand the topic, we use a transmitter whose factory setting is 1 Hertz as the live broadcast transmitter. Such a transmitter will emit one wavelength every second. Such a low frequency value will be insufficient to convey the image of the clock. But it will be able to send the information on time that belongs to the clock in a very sensitive way.

In the figure below, we see clock signals going from the signal tower towards three different frames. The wavelengths of the signals that set out from the transmitter and go to the planes that are in motion will change as we saw before. The wavelength of the signals that set out at (c+v) speed and go towards the plane which is moving away will get longer while the wavelength of the signals that set out from the transmitter at (c-v) speed and go towards the plane which is approaching will get shorter.



We can easily calculate the amount of wavelength changes by making use of Doppler equations, but as our topic is Time Shift, let’s describe the wavelength changes depending on time this time. Wavelength is a distance value. There is a basic equation between distance, speed, and time.
Distance = Speed x Time
Therefore, we can write the wavelength of the signal that set out from the transmitter depending on the emission speed and emission duration. Assume that the emission duration of a single wavelength that belongs to the signal is “t0”. According to this, the lengths of wavelengths will form as shown below. We already know that the emission duration of the wavelengths for the three equations will not change because their emission frequencies are equal.



Now, let’s write in how much time is the signal that is equal in length to the wavelength received at the arrival target. Because incoming signal speed is always constant and “c”, the duration of receiving of the wavelength will be as follows:



The situation described above is shown in the below figure.



We see that, if a signal is going towards a target that is in motion, there occurs a difference between the duration of signal emission at the source and the duration of receiving of the signal at the target. This difference is the cause of the event called Time Shift. Time Shift should not be confused with the time that passes for a signal to travel to its target. Time Shift determines the speed of flow of time of Visible Time on Image Object.

Firstly, let’s write the basic equations that give us Time Shift by making use of the figure above.




 [1]
[1]

Wavelength change is calculated with  [2] . By using [1] and [2] we can formulate the equation above based on the wavelength as follows:
[2] . By using [1] and [2] we can formulate the equation above based on the wavelength as follows:


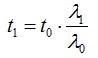 [3]
[3]

t0 : Duration of wavelength emission
t1 : Duration of receiving of wavelength
λ0 : Factory setting of the transmitter's wavelength
λ1 : Wavelength of a signal that sets out from the transmitter and goes to a target that is in motion
c : Light speed constant
v : Difference between the source emitting the signal and the arrival target of the signal
c±v : The speed of signal emission

We obtained the equations below for Time Shift.



“t0” value that describes the duration of wavelength emission gives the information about the time of the event occurring in Source Object in Absolute Time and represents Absolute Time. Duration of receiving of wavelength also occurs in Absolute Time and it basically determines the speed of flow of time on Image Object and represents Visible Time. The difference between these two times gives the amount of Time Shift.



The mathematical expression of this equation is as follows:

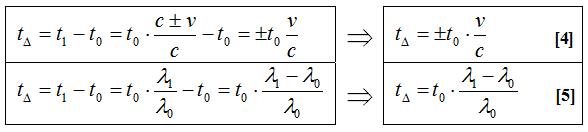

At the top right expression written based on the speeds, the equation gets “+” value for reference systems that move away from each other and “-” for reference systems that approach each other. Positive tΔ value shows the speed of flow of Visible Time slows down and negative tΔ shows that speeds up.

If we pay attention, t0 is a value that occurs based on wavelength
(t0 = λ0/c) .
Therefore, we can use the equation for any wavelength. Arbitrarily, we can image a wavelength as "λ0/c = 1 second", and even "λ0/c = 1 hour". What I am trying to tell you is this: In equations [4] and [5], we can use any time duration for
t0 value. If we accept t0 = 1 seconds, we find the Time Shift that occurs in a duration of 1 second.

For instance, let’s calculate Time Shift difference for a second for a meteor that moves at 30.000 km/sec.
Time Shift Difference = 1 . (30.000/300.000) = 0.1
And this makes 6 seconds in a minute. If we put a clock on the meteor and observed the clock from a screen on earth with live broadcast, we would see that the clock loses 6 seconds per minute if the meteor is moving away from us and that the clock gains 6 seconds per minute if the meteor is approaching us. Let’s assume that an observer looking at the meteor from earth observed a blow-out of gas on the meteor. The speed of flow of time of this event will be subject to a difference of 6 seconds. Time Shift is like watching a movie in slow motion or fast motion. Image Objects of objects that are in motion always have the event of Time Shift in themselves.

Naturally, it is almost impossible to observe Time Shift with the naked eyes because, for an event that we can observe, the speeds should be extremely high. How can our eyes observe Time Shift when they cannot observe a bullet fired? But this is not the case of communication signals. Sensitive devices can immediately detect Time Shift. Time Shift explicitly shows itself in satellite communications, interstellar travels, and even in communication between high-speed planes.

21.1. SPEED OF FLOW OF TIME CONVERSIONS BETWEEN ABSOLUTE TIME AND VISIBLE TIME

As mentioned in “Time Shift Difference", we can directly find the amount of change in the speed of flow of time by putting any time value in place of t0 or t1 values in the equations below.



Let’s give an example. Assume that we are watching an event that lasts 20 minutes in an Image Object. We want to find in how much time this event occurs in Absolute Time (in other words, in Source Object, namely in reality).
Let’s say λ0 = 15nm, λ1 = 16nm. (Since λ1> λ0
Source Object is moving away.)
We are looking for t0 value here . Then t0 = t1 . (λ0 / λ1)
.
t0 = 20 . (15 / 16) = 18.75 minutes = 18 minutes and 45
seconds

As seen in the calculation above, we can formulate the conversions between Absolute Time and Visible Time in the way as described below. In the equations,
t0 value represents Absolute Time and t1 value represents Visible Time.



In the calculations where speed values are used instead of wavelength, “v” value that represents the speeds of frames relative to each other should be calculated first. How this calculation was done was covered before.

21.2. LIMITS OF THE SPEED OF FLOW OF VISIBLE TIME

The table below is an important table in that it shows the theory of speed of flow of Visible Time. It was generated as a result of the equation
t1= t0.(c±v)/c. It shows the equivalent of 1 second which is in Absolute Time in Visible Time.



There is no theoretical limit to the speed of flow of Visible Time. It is possible to extend the table in both directions. We can do this extension by adding +2c, +3c, +4c, etc. on its right side and -2c, -3c, -4c, etc. on its left side for the v value. I prepared the table this way in order to make it look balanced. “+v” values in the table indicate that two objects that are in motion relative to each other are moving away from one another and “-v” values indicate that the two objects are approaching each other.

“1” value in the line “Speed of Flow of Time” in the table shows that two objects are motionless relative to each other. In this case, the speed of flow of Absolute Time is equal to the speed of flow of Visible Time. In every case except this, the speed of flow of Visible Time is different from the speed of flow of Absolute Time or the direction of the flow of Visible Time is in backward direction.

The values on the right side of “0” point in the line Speed of Flow of Time shows that Visible Time flows forward (which is the regular direction of flow of time) and the values on the left shows that Visible Time flows backward. If two objects are approaching each other at a speed more than the speed of light (exceedance of -c speed), the direction of the flow of Visible Time is reversed. (Like watching a movie from the end to the beginning.)

In the line Speed of Flow of Time, the values between “-1….1” shows that the speed of flow of Visible Time is faster than normal. When we get closer to 0 value from both directions, the speed of flow of Visible Time gradually increase. Around “0” point, time flows at infinite speed. When you reach “0” point, the speed of flow of Visible Time stops completely. In this special case, two objects are approaching each other at the speed of light. Since the speed of the movement of the signal is equal to the speed of the object that sends the signal, signal transfer doesn’t take place and Visible Time stops as a result of this.

The values that are out of the range “-1….1” shows the slowdown in the speed of flow of Visible Time. The more you move forward to values smaller than -1 and values bigger than 1, the more the speed of flow of Visible Time slows down. -1 value is the same with a time of 1 second as duration, but the direction of the speed of flow of time is backward.

For instance; let’s choose +0.5 and -0.5 values for t1 values. These values will show us that duration of one second in Absolute Time will pass in half a second in Visible Time. These are equal speeds of flow of time. However, Visible Time flows forward in one of them and flows backward in the other. The speed of flow of Visible Time increased in both cases.

Our life goes on in a very narrow range on the point where 1 value is in the line Speed of Flow of Time. In practice, because “v” values that we can reach are too small compared to the speed of light, the speed of flow of Visible Time changes very little and can only be detected with sensitive devices.

21.3. WHAT TIME IS IT THERE?

Let’s say A and B are two objects that are in motion relative to each other. Since these two objects, just like all objects, need to perform their movements in Absolute Space-Time, it is not possible for the Source Objects of these two objects to have differences in terms of the time zone they are in. From this point of view, it is extremely easy to give an answer by looking from the side of Absolute Time. If the time is 03:00:00 in A, it is 03:00:00 in B, as well. Their speeds, the position they are in space, directions of their movements, whether they have accelerated movement, whether the distance between is a few meters or hundreds of light years; nothing can spoil this synchronization.

Therefore, the question “What Time Is It There?” generally carries this meaning:
What is the time that an observer sees or perceives on a clock that is at a different location? And this describes a situation such as this: What is the time an observer sees on an Image Object? This is the real question that we need to answer.

Now that the distance between Source Object and Target Object and the signal speed together determines the arrival time of the signal, we can calculate the delay in time from this point of view and find in which time zone the Image Object is in. When we divide the distance between Source and Target objects by the signal speed, the value we get is the arrival time of the signal. Our job will be to reach Visible Space-Time based on Absolute Space-Time. Here we will summarize the general rules that we saw before. The signal speed will be formed according to the rules of (c+v) (c-v) mathematics.

The time of signal arrival between Source Object and Target Object is as follows.
But this equation doesn’t show the arrival time of the signal that sets out from the source; it shows the arrival time of the signal that has reached its target.

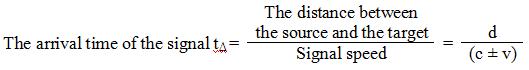

The tΔ obtained here gives us the delay time. When we subtract tΔ time from Absolute Time, we find what time is it at Image Object.



As there is time unity between Source Objects for Absolute Time, we can use the value of our own clock (We ignore the time that passes in order to perceive what time our clock shows.)



Now, with the help of the figure below, let’s find out the location of the Image Object and the time at the Image Object by using the Source Object. Assume that the Source Object goes at “u” speed and that it is at Point C at this moment. The observer at Point A sees the Image Object at
d1 = c . tΔ distance from itself and at the Point B which is
d2 = u . tΔ distance behind Point C. The signal sent by Source Object when it was at Point B is the signal that determines what time it is at the Image Object. When the signal reaches the observer that is at Point A, the Source Object will be at Point C and the Image Object will be at Point B.



As seen in the figure, a “Doppler Triangle” is formed. Here we consider Absolute Space-Time as the starting point and we applied the rules to reach Visible Space-Time. But, of course, we don’t have the chance to apply this rule in such an order in practice because Absolute Space-Time is abstract for us. In the example here, the observer at the Target Object cannot see the Source Object at Point B, either. However, the observer will see its Image Object at Point B when a time as much as tΔ passes.

We can easily say the following as a conclusion from the figure. An observer can easily find what time it is in the Image Object by dividing the distance that it has from the Image Object that it sees by the speed of light constant. And because the Image Object can be seen, the distance between can generally be measured. The value that the observer gets after the division is the arrival time of the signal. If the observer subtracts this time from the value of his own clock, he will find what time it is in the Image Object.

In this way, we reached the same result based on not only the Source Object but also the Image Object, and we had to reach this result anyway, because we have the following equation for tΔ in a Doppler Triangle (if we use the figure above as a base).



We can present this equation as below:



Finally, the answer to the question “What is the time on an Image Object?” is as follows:



The meaning of this equation in practice is
below.



Lastly, let’s write the speed of flow of Visible Time.
The speed of the flow of Visible Time on Image object has gone through
t1=
t0. (c+v)/c change in a second.

